UNISCI I PUNTINI E RIPRODUCI LE FIGURE

Materiale

Età

Numero di giocatori

Competenze acquisite
INTRODUZIONE:
Per svolgere ognuna delle tre attività seguenti è bene che l’insegnante legga e spieghi in dettaglio le regole agli studenti. E per facilitarne la comprensione è invitato a mostrare sempre l’esempio con soluzione presente a inizio di ogni attività. Inoltre l’insegnate, se vede che l’intera classe presenta delle difficoltà nel risolvere le sfide presenti, può di volta in volta, possedendo le soluzioni, dare degli aiutini o suggerimenti.
Iniziamo l’attività facendo un’introduzione semplice e divertente per gli studenti in modo tale da attirare la loro attenzione.
Per svolgere questa introduzione all’attività, bisogna rispettare le seguenti semplici regole:
- Tra i vari puntini che abbiamo a disposizione si cerca il puntino numero 1, che indica il punto di partenza della figura
- Con la matita, seguendo la numerazione e senza staccare la punta dal foglio, si uniscono tutti i puntini fino a completarla.
L’insegnante legge e descrive in maniera dettagliata agli studenti le regole che devono essere rispettate per svolgere l’attività, e per aiutarne la comprensione può eseguire l’esempio alla lavagna.
Esempio del funzionamento per l’insegnante:
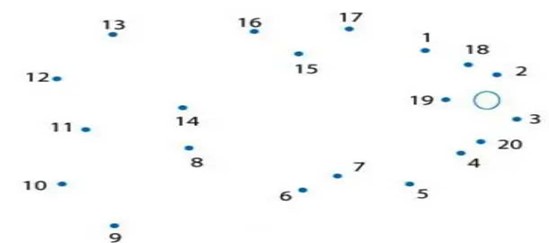
1
Esempio per l’insegnante da mostrare agli studenti; quelli mostrati di seguito sono i puntini che dobbiamo unire:
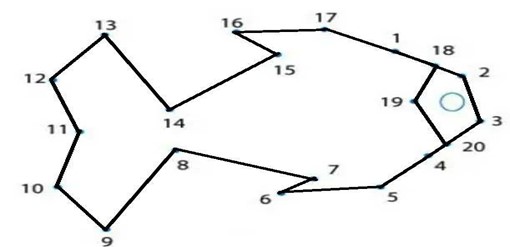
2
Quindi se seguiamo le due regole osservate in precedenza, ovvero partire dal numero 1 e seguire la numerazione senza staccare la punta della matita dal foglio, senza fare troppa fatica arriveremo al seguente risultato:
Ora tocca agli studenti:

1
Dopo aver terminato la spiegazione, assegnate a ogni studente il seguente foglio di lavoro, e dite
loro di svolgere la stessa attività svolta dall’insegnante poco prima.
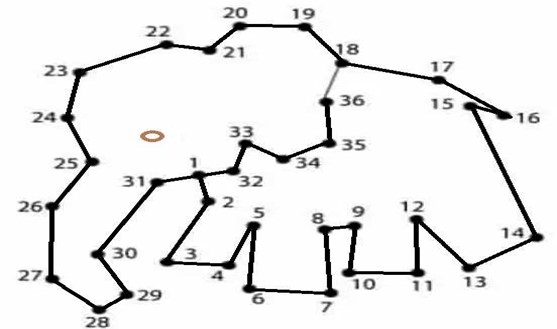
2
Dando loro un po’ di tempo, dopo che tutti gli studenti avranno terminato l’attività, l’insegnante mostrerà la soluzione alla lavagna.
DESCRIZIONE DELL’ ATTIVITÀ:
Terminata la parte introduttiva, passiamo ora a qualcosa di leggermente più complesso, ma sempre altrettanto divertente
Regole da rispettare per svolgere l’attività:
- Osservare bene la figura proposta che bisogna produrre
- Tra i vari puntini presenti scegliere a piacimento un puntino da cui si vuole partire
- Partendo dal puntino scelto e senza staccare la punta della matita dal foglio unire tutti i puntini e riprodurre la figura
Prima di iniziare dividiamo l’intera classe in gruppi da due studenti. In ogni gruppo, gli studenti possono ragionare insieme la possibile soluzione; durante lo svolgimento uno dei due studenti deve tenere traccia dei passi fatti per arrivare alla soluzione, ovvero mano a mano che uno studente svolge l’attività l’altro studente oltre a cooperare con il ragionamento numera l’ordine delle linee tracciate. Altrimenti si rischia di arrivare a una soluzione e non ricordare i passi fatti per arrivarci.
L’insegnate legge e descrivete in maniera dettagliata agli studenti le regole che devono essere rispettate per svolgere l’attività, e per aiutarne la comprensione, è consigliato eseguire un esempio alla lavagna.
Esempio del funzionamento per l’insegnante:
1
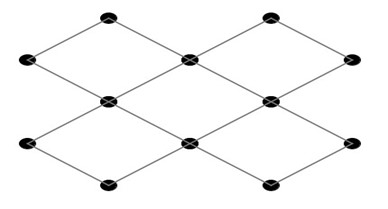
Mostrare agli studenti la figura che dobbiamo riprodurre:

2
Qui troviamo invece i puntini che bisognerà unire per formare la figura che si è appena osservata, ovviamente bisogna rispettare le regole viste in precedenza altrimenti il gioco non è valido; ovvero osservare la figura da riprodurre, scegliere un puntino da cui si vuole partire e unire i vari puntini per formare la figura senza mai alzare la punta della matita dal foglio.
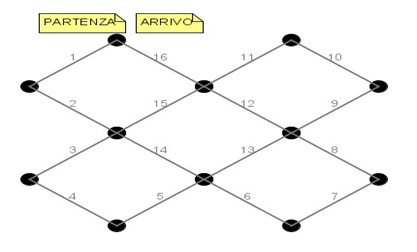
3
In questo caso, ci sono più soluzioni possibili per l’attività; una delle possibili soluzioni è la seguente:
Dopo aver terminato la spiegazione, assegnate a ogni coppia di studenti uno dei fogli di lavoro, e dite loro di svolgere la stessa attività appena spiegata.
ANCHE QUESTA È INFORMATICA!
Le due attività appena viste, sono utili per andare a introdurre un concetto fondamentale in informatica ovvero la Teoria dei Grafi che è la disciplina che si occupa dello studio dei Grafi. In informatica un Grafo è formato da un insieme di elementi detti Vertici o Nodi che possono essere collegati tra di loro da linee chiamate Archi o Lati. Graficamente i Vertici/Nodi sono rappresentati con dei cerchi con dentro un nome, che può anche essere una semplicissima lettera o numero; mentre gli Archi/Lati sono delle linee che mettono in collegamento due vertici e delle volte sopra hanno un numero che indica il costo che si ha se lo si percorre. Il numero di archi che confluiscono in un vertice viene chiamato Grado del Vertice.
Troviamo due tipi di grafi:
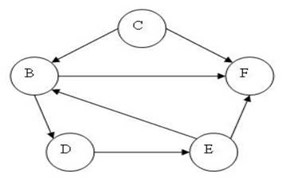
Orientati
Grafi i in cui gli archi hanno una freccia ad una delle due estremità che serve per indicare il verso di percorrenza di tale arco;
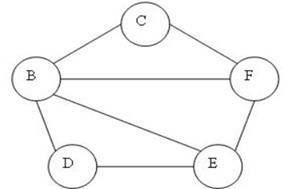
Non orientati
Come suggerisce il nome stesso, in questi grafi gli archi possono essere percorsi in qualsiasi direzione, da sinistra verso destra o viceversa;
Nella teoria dei grafi troviamo il seguente enunciato di Eulero:
Un qualsiasi grafo è percorribile se e solo se ha tutti i vertici di grado pari, oppure se solo due di essi sono di grado dispari; inoltre se ci troviamo nel secondo caso per poterlo precorrere è necessario partire da uno di essi e al termine del percorso ci ritroveremo sull’altro vertice dispari.
Questo significa che un grafo che ha:
- Tutti i Vertici di grado pari è sempre percorribile indipendentemente dal vertice da cui si parte.
- Due soli Vertici di grado dispari e tutti gli altri di grado pari è percorribile a patto che si parta da uno dei due vertici di grado dispari e al termine si arriverà sull’altro vertice di grado dispari.
- Tutti i Vertici di grado dispari oppure tre o più vertici di grado dispari non è mai percorribile indipendentemente dal vertice da cui si decide di partire.
DOMANDA:
In questa attività dove trovo tutto questo?
Attività – Unisci i puntini e riproduci le figure
- Vertici/Nodi: sono i puntini neri
- Archi/Lati: son le linee da voi tracciate per riprodurre la figura
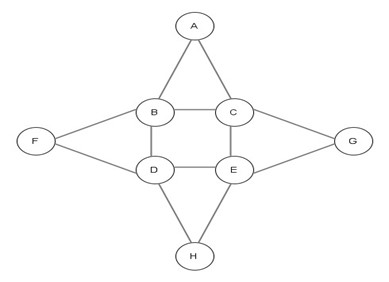
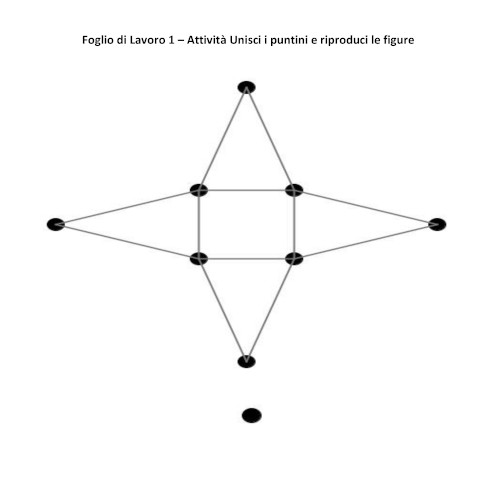
Foglio di lavoro 1
I Vertici sono tutti di grado pari, è sempre percorribile, infatti indipendentemente dal puntino in cui gli studenti scelgono di partire, c’è sempre almeno una possibile soluzione.
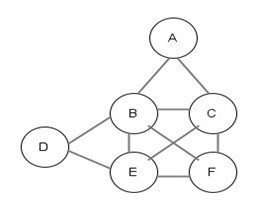
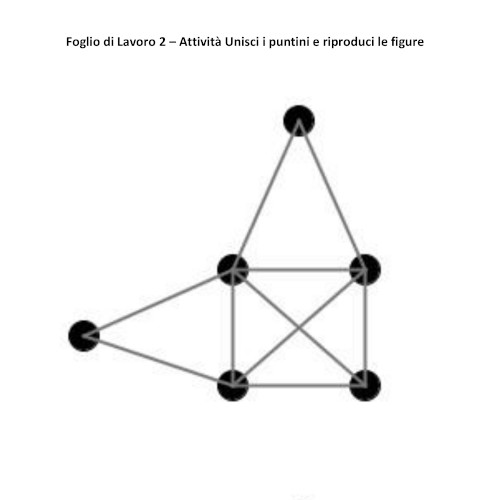
Foglio di lavoro 2
I Vertici sono due di grado dispari e gli altri di grado pari, è percorribile se è solo se si parte da uno dei due vertici di grado dispari, infatti gli studenti riusciranno a trovare una soluzione alla sfida se e solo se partiranno dai puntini giusti, altrimenti non giungeranno ad una soluzione.
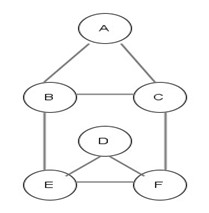
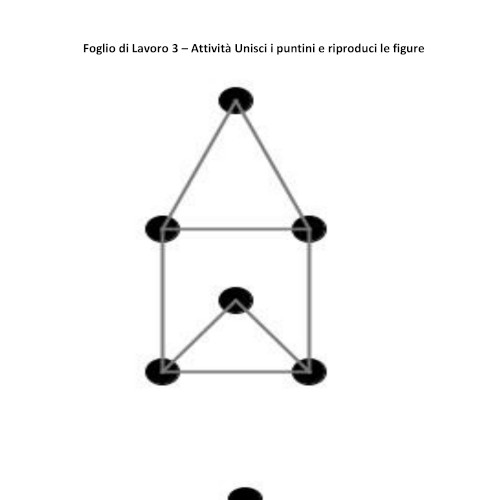
Foglio di lavoro 3
I Vertici di grado dispari sono più di due, non è mai percorribile, infatti gli studenti indipendentemente da dove decideranno di partire mai riusciranno a risolvere la sfida.
Ma perchè la teoria dei grafi e i grafi sono così importanti?
Perché nel nostro mondo innumerevoli situazioni possono essere modellate tramite il loro utilizzo. Esempio: la progettazione delle connessioni di una rete informatica, la progettazione di rotte di navi o aerei, la progettazione di come posizionare le strade in una città, la progettazione della copertura di una rete di trasporti pubblici (metropolitana, pullman, treni), nei giochi (come abbiamo appena visto) e in tantissimi altri contesti.